Figure 2C

For the \(\alpha\), \(\beta\) pairs created for Figure 2B calculate \(\varrho\) as

\begin{align} \varrho = \frac{\int_0^1 x^2 f^T_{\alpha,\beta}(x)\,dx}{\left(\int_0^1 x f^T_{\alpha,\beta}(x)\, dx\right)^2}, \end{align}

and save the results. This takes some time.

import numpy as np

from gamma_functions import *

import scipy.integrate as integrate


a_ns = np.load("data/a_ns.npy")
b_ns = np.load("data/b_ns.npy")

rhos = []

for a,b in zip(a_ns,b_ns):

    numer = integrate.quad(lambda x:x**2*fT(x,a,b),0,1)[0]
    denom = (integrate.quad(lambda x: x*fT(x,a,b), 0,1)[0])**2

    rho = numer/denom

    print a, "\t", b, "\t", rho

    rhos.append(rho)

np.save("data/rho_theoretical.npy", rhos)

Then, to get

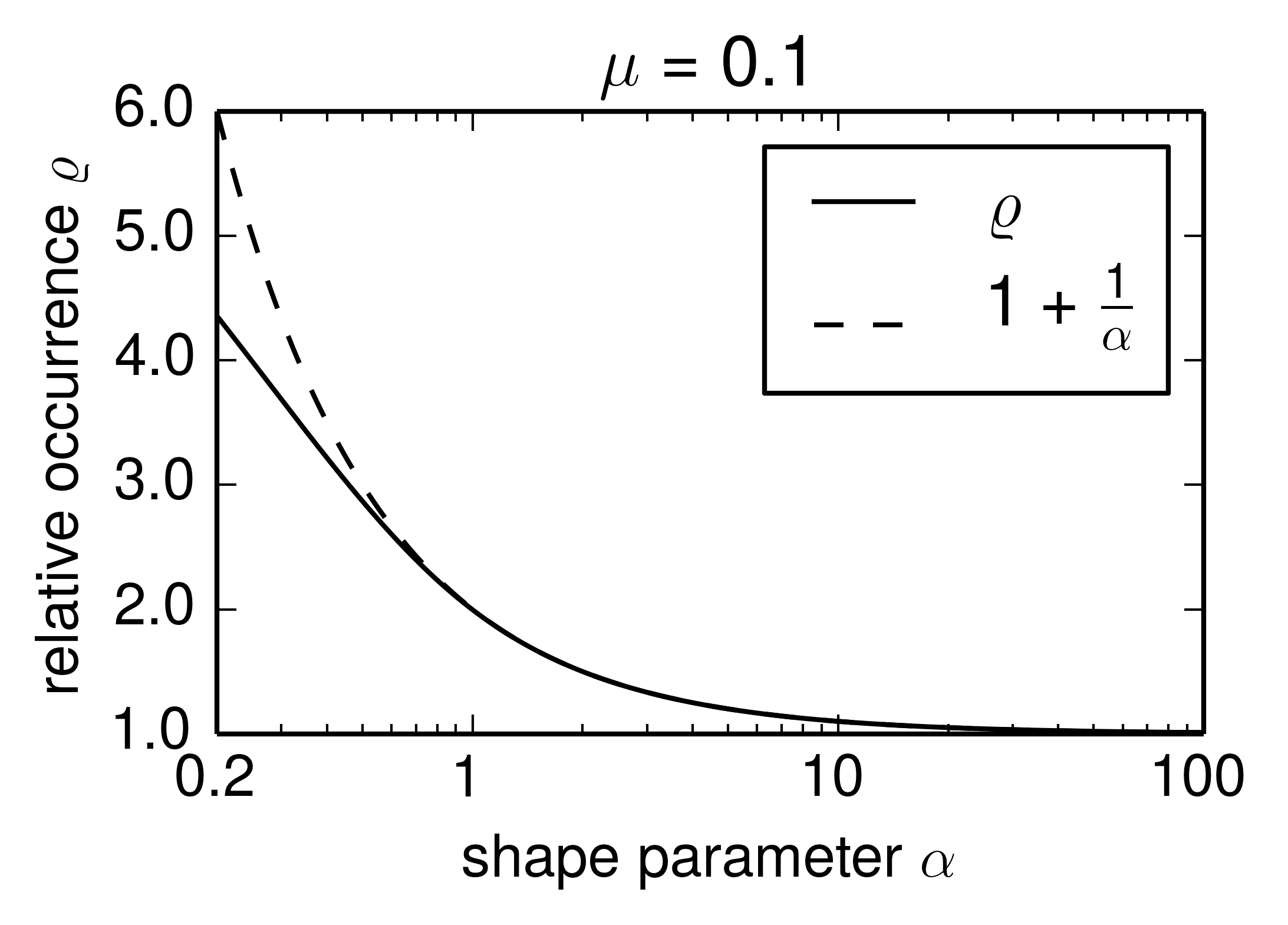
for given \(\alpha\) plot the \(\varrho\) as calculated a above and compare with the approximation \(1 + \frac{1}{\alpha}\).

import pylab as pl
import numpy as np

from scipy.stats import gamma

import matplotlib.ticker as ticker
from matplotlib import rc

rc('text', usetex=True)
pl.rcParams['text.latex.preamble'] = [
    r'\usepackage{tgheros}',    # helvetica font
    r'\usepackage{sansmath}',   # math-font matching  helvetica
    r'\sansmath'                # actually tell tex to use it!
    r'\usepackage{siunitx}',    # micro symbols
    r'\sisetup{detect-all}',    # force siunitx to use the fonts
]  


a_ns = np.load("data/a_ns.npy")
rhos = np.load("data/rho_theoretical.npy")

fig, ax = pl.subplots(1,1)
fig.set_size_inches(7.2*0.5,2.2)

ax.plot(a_ns,  rhos , color='k', label=r'$\varrho$')
ax.plot(a_ns, [1+1./a for a in a_ns], color='k',
        linestyle='dashed', label=r'$1+\frac{1}{\alpha}$')

ax.set_title(r'$\mu = 0.1$')

ax.set_xscale('log')
ax.set_xlabel(r'shape parameter $\alpha$')
ax.set_ylabel(r'relative occurrence $\varrho$')

pl.yticks(list(pl.yticks()[0]),
          ['%.1f' % tick for tick in pl.yticks()[0]])

pl.xticks(sorted(list(pl.xticks()[0]) + [0.2]),
          sorted(['0.2']+[str(int(x)) for x in list(pl.xticks()[0])]))

ax.set_xlim(0.2,100)

ax.legend()


pl.savefig('gamma_figC.pdf', dpi=600, bbox_inches='tight')